这是一篇迟到的总结,其实今年2月就已经赢了的。写这个总结是为了详解打僵尸程序 的进化过程,帮大家看懂它的战术和走位。
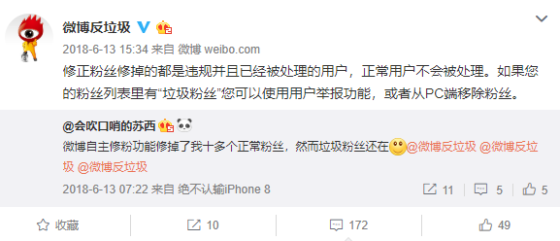
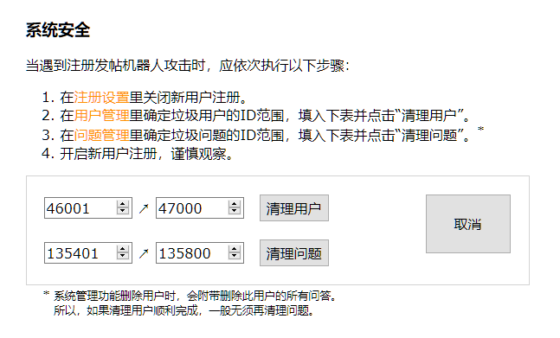
众所周知,渣浪微博的僵尸化很严重,并且渣浪无计可施。很多人以为“微博反垃圾 ”有用(起初我也这么以为),但微博反垃圾这样解释自己的功能:
也就是说,当某用户被举报封号时,渣浪并不会及时清理它和正常用户的关注/被粉关系,直到该用户手动修正粉丝为止(并且只修好他自己的)。其实这是把流程缺失的责任转嫁到用户身上。并且,从这个解释来看,让绝大多数人头疼的僵尸粉,在渣浪眼里是正常用户:不说话当然不会被举报封号啦。
第一次使用微博反垃圾的,会很欣喜,因为立竿见影,一下子粉丝数就降下来了。那是当然,堆积N年的陈年老尸,被火化时肯定狼烟滚滚。但再使用时,它只能帮着清掉从上次大扫除以来积累的垃圾,效果就会令人失望了。
所以我决定自己搞定这件事。从去年11月开始,用Python语言写了个程序,中间随着战斗局势变化,修改几回。大约到了12月中,程序功能基本上就是今天的样子了。
我把僵尸粉分为这样三种:
经典僵尸,就是简单地沉默寡言。 打榜僵尸,“They were once men.” 结群抱团滚滚而来,发博量如超新星爆发。爱豆活动一结束,立即坍缩成黑洞。爆发时显得脑残,坍缩后更像垃圾。 自语僵尸,程控喃喃自语,诉说爱情痛楚和人生感悟,每天一两次,莫名瘆人。这也是目前卖粉的主打产品。 对这三种僵尸的识别处理,是推进程序的主要动力。下面细说程序的演化过程。
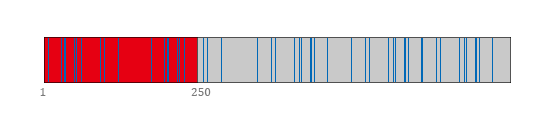
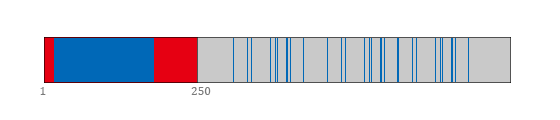
首先说说起始状态。一个被僵尸粉占据的帐户,其粉丝列表大约是这样的结构:
被僵尸攻陷的粉丝列表,数字是页数 图中,红色代表僵尸,蓝色代表正常粉丝,灰色代表250页之后、被渣浪隐藏的粉丝列表(可以想象,其中的僵尸依然是多数)。数字是粉丝列表的页数。渣浪的规则:即使看自己的粉丝列表,也只能看至多250页,每页20个(即最多5000个)。假如看别人的,则最多只能看5页(100个)。
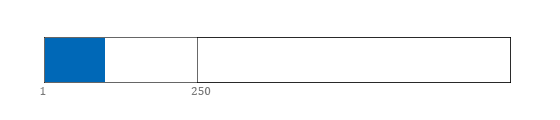
我们期待的理想健康状态,当然是下图这样的,红色泡沫被挤空,蓝色真粉致密地聚集在一起:
健康状态的粉丝列表 知道了自己在哪儿,目标在何方,就可以着手制订路线,准备工具。
最初考虑的是渣浪自己的微博API ——它自己家的东西嘛,用起来肯定最趁手。但仔细阅读其功能后就会发现,根本没有删除粉丝的接口(曾经有,后来撤了 ,让人高度怀疑,僵尸粉都是渣浪自己喂养释放的)。
那就只能自备工具了,我使用早有成熟功能库的Python + Selenium。
和网络相关的编程,最简单直接的操作是“访问链接”,于是,可行性预研从这个办法入手。经过调研发现,“访问1个链接就能删除1个粉丝”的功能,在手机浏览器彩版微博 (不是手机客户端)可以实现,但彩版微博最多只给看1000个粉丝。
所以程序最初分为两节:第一节从网页版微博抓取粉丝列表(至多5000个),分析僵尸后写进数据库。第二节读取数据库,把标记为僵尸的,通过访问彩版微博删除。删除之后,前250页留下的空位,会从原本隐藏的地方(上面图中所示灰区)抽调名额填补,这样就又可以循环以上过程,轮转不已。
这个方法确实有用,帮着我删除了最初一两千个。还让我发现,刷页不能过快,否则会被微博拒访几分钟。最初的删除速度,可以点这里 了解,但此视频的续集就是几分钟的空白页面,飞速删除所节省的时间全赔进去了。从此,大约两秒1个的“稳健”速度一直保持到最新版。认为这个程序不够快的用户,读到这里应该能理解了。
接下来,我开始对程序的分节运行感到不爽。眼前分明一群僵尸,却要等几十分钟后才能看到它们被删除。更重要的是,抓取和删除间隔久远,谁冤枉了,谁漏网了,根本对不上号。所以我开始做即见即删的版本,看到僵尸就立刻操纵鼠标去打开菜单,点删除按钮,不再攒到一起秋后问斩了。
拉菜单点按钮敲回车的操作当然要比访问链接复杂得多,幸好Python + Selenium的功能还挺齐全,很快就搞定了改写工作。
最初程序分两节运行时,只要能把粉丝列表逐页看完就行, 正着看倒着看并不重要 。但到了即见即删的阶段,访问顺序就变得很重要。即见即删的第一版继承了正向浏览的基础,那时的工作方法是:浏览第1页,删除本页上的僵尸,腾出空位来了,刷新本页,把原在第2页的粉丝填上来几个,再删再刷,直到本页全是活粉,再挪到第2页如法炮制。
说真的,假如不考虑效率的话,这个操作过程比现在的版本还花样繁多,令人沉迷,每次运行时我都能盯着看很久。也正是因为看很久,看出问题了:20个位置,前19个都坐满了活粉,只剩1个空位时,程序还不屈不挠地刷呀删呀,每刷只能删1个,太弱智了。
于是做了个改写,每次从250页逆行到第1页,刷完删完不停留,继续上行。这样每次看到的都是新面孔。当有僵尸从第1页正门持续涌入时,逆流而上更是所见常新。程序朴实了,却变得高效。
读到这里,用户应该明白为何程序总是从后往前扫了。至于每次开始程序总是先看第1页,那是因为要读取最大页码,好知道从哪里开始做起。
逆向即见即删版做完后,程序夜以继日地干活,很快把粉丝删成了这样的分布:
典型的删粉进度 这是一个典型的删粉进度。大蓝块是沙里淘金浓缩成的活粉大军,它左边是正门涌入的僵尸粉,右边是有待处理的旧僵尸。
这时我开始担心两件事:一是假如程序还这么傻不拉几地从250扫到1,那么它的大部分时间会浪费在活粉大军上,并且越来越耗时。二是最终删成下图这样时,前250页挤满了活粉,按关注时间排序的新僵尸只从左边进,旧僵尸从右边冒不出来,程序必然熄火。
熄火状态 第二个问题无计可施(也就是说,真粉极多的大用户,不要指望这个程序带来太大的改观),先解决第一个。我在程序里加了几段代码,让它一旦撞到大蓝块,就指数级速降,尽快跳到粉丝列表的头3页去工作。每清完头3页,就相当于把大蓝块往左拽一拽,从右边抽出更多的粉丝列表来。反正在活粉大军前面干活也是干,后面干活也是干,都没有浪费宝贵时间。
读到这里的用户应该能明白,为何250、249之后,突然就skipping active fans,快速地跑到第3页去了。也会有用户问,可有时程序还是继续老实巴交地248、247、246呀。那是因为我担心有些“活粉”会退化成僵尸,所以安排了5%的概率,让程序重新审视活粉大军,看看有没有蜕变了的。
说到活粉的退化,就要谈谈僵尸的定义了。最原始的定义当然是发博少,但怎么才叫少?注册10年的用户发10帖可以称作少,而来微博刚俩月的,发10博就还算可以了,所以发博量要用注册时间来衡量。准确的注册时间并未体现在粉丝列表里,不过从此人ID上可以看出来。通过采集大量的数据,我得到了这些信息:
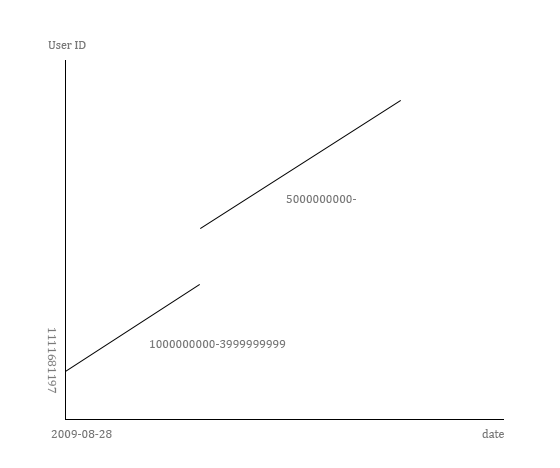
可以用“来去之间”的ID和注册时间作一个基准(早于他的可斜率外推)。 微博每天用户增长量大约是1,418,780个。 渣浪的用户ID没有4开头的,4000000000-4999999999这段ID不存在。 这些信息给了我一个经验公式。从粉丝列表读到他们的ID时,我大致可以知道他们何时来的微博,再按照每月一博的标准(很宽容了)来衡量,低于这个阈值的,就判为僵尸删除掉。
用户ID和注册时间的对应关系 所以,随着时间的流逝,曾经的活粉退化为僵尸是很有可能的。有人会说这是误判,但我认为,一个人如果喜欢潜水——后面会提到,一些僵尸都比他活跃——那么他对被粉的博主只是日常“视奸”,并未传播博主的信息,留他何用呢?
再说打榜僵尸。这些帐户的存在通常和某明星或某活动有关,是买来的帐户。在演唱会、见面会开始之前,异常活跃。并且抱团互粉,同进同退。单单从粉丝量、关注量、发博量上来看,都不易判为僵尸。下图是一坨样本。
打榜僵尸团样本 严格来说,他们并非僵尸,结群出现到处留言点赞,无非是想吸引你点开他们的页面,看看他们爱豆的最新动态。但他们是为爱豆来的,与我无关,留他们干嘛呢?
单从数字上识别这一类的僵尸很不容易,活动进行期间更是不可能,结群出现时容易感知其命名规律,但这种规律经不起时间考验,不能放到打算长期运行的程序里。幸好活动一过,他们就会闭嘴。于是,我在程序里做了一个新动作:翻检每个粉丝的主页,如果他们持续静默3个月,就判为僵尸。右图里的这些ID,在新规则出台后很快被删了个一干二净。
翻检主页的动作比较耗时,所以程序只在闲时才做。当它扫完一页,没看到经典僵尸时,就会认为咖啡时间到,从数据库里挑选10个最近没看过的ID,一个个翻阅其主页。“微博会员升级啦”、“生日快乐”、“抢了个大红包”这一类的自动信息不计入此人发帖。
读到这里的用户,应该能明白为何程序忽然不刷粉丝列表,而是去浏览用户主页了。
羽翼初丰的程序刚刚开开心心地运行了两三天,我遭遇了来自渣浪的第一次打击:它只给我看两页粉了 !这种情况相当于提前进入了被活粉憋死的熄火状态(想象一下上面熄火图中的250改为2)。很有可能是前期可行性测试时,对微博访问过频,被渣浪的系统安全机器人留意到了。
挑战也是机遇嘛,逼迫我提前考虑如何在熄火状态下持续工作了。最终发现,“按最近联系人排序”的话,互动粉丝列表(最多50页)的后半段还能看到许多僵尸粉(并未互动过)。这个列表不会实时更新,删除僵尸后,第二天大约同一时间才会填充新的。不过,每天还能删大约500个,聊胜于无呀。
读到这里的用户应该能明白,为何程序一上来就先从第50页扫描互动粉丝列表了,而且一旦扫完,8小时内不会再碰。昨天有个用户哭着对我说,为什么要删互动粉丝啊?他们都是活粉真粉啊!我拿到她的活粉样本一看,2010年注册的,发帖24,僵尸都更活泼些……
还有潜水员一听我要打僵尸,马上跑来评论:“真粉报到!”“我是活的!”他们假如不吭气还没事,一说话,第二天就上了互动粉丝列表,被程序看到了,发博数本身就可疑,再翻翻主页三个月没说话,就手起刀落了。
同样,我不把这些叫冤杀,如果不想被判为僵尸粉,应该活出自己的精彩来,经营好自己的地盘,不要只在别人家做客。
对于活粉很多的大用户——哪怕僵尸也很多——相信活粉还是能挤满50页(1000个座位)的,这个放僵尸的门缝可能并不存在。
熄火运作了将近1个月,渣浪忽然又开放了250页列表(后来这类事情又发生过两次),迎来了重新开工后的大高峰。
熄火→开工大爆发 从此僵尸粉一溃千里,今年2月,最终删到了5000以下(250页以内),所有粉丝都移出灰区。终于有把握说,我赢得了这场打僵尸的战役。
此后又有几个次要更新,包括对“真是活人”的提前赦免,以及对自语僵尸的判断(逻辑尚在试运行中),都是细枝末节的事了。
最近有些饱受僵尸困扰的用户来下载使用这个程序,有一些给我的反馈里,提出了很好的建议,打开了新的思路。例如,自语僵尸,我这里没几个,而在别人那里则是主要问题。也有抱怨声,比如程序有点慢,为什么要翻看主页,为什么冤杀活粉,等等。我想说,僵尸没有一定之规,几套判断逻辑互相辅助制衡,共同把僵尸逼上绝路,推敲了大半年。随着局势变化,有些看似漫不经心的流程会渐渐凸显其作用。都是我亲自趟过的坑,好不容易填平了的,请不要再把我拽回坑里去了。